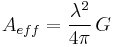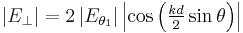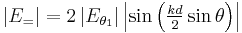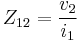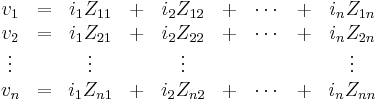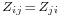Antenna (radio)
An antenna (or aerial) is an electrical device which converts electric currents into radio waves, and vice versa. It is usually used with a radio transmitter or radio receiver. In transmission, a radio transmitter applies an oscillating radio frequency electric current to the antenna's terminals, and the antenna radiates the energy from the current as electromagnetic waves (radio waves). In reception, an antenna intercepts some of the power of an electromagnetic wave in order to produce a tiny voltage at its terminals, that is applied to a receiver to be amplified. An antenna can be used for both transmitting and receiving.
Antennas are essential components of all equipment that uses radio. They are used in systems such as radio broadcasting, broadcast television, two-way radio, communications receivers, radar, cell phones, and satellite communications, as well as other devices such as garage door openers, wireless microphones, bluetooth enabled devices, wireless computer networks, baby monitors, and RFID tags on merchandise.
Typically an antenna consists of an arrangement of metallic conductors ("elements"), electrically connected (often through a transmission line) to the receiver or transmitter. An oscillating current of electrons forced through the antenna by a transmitter will create an oscillating magnetic field around the antenna elements, while the charge of the electrons also creates an oscillating electric field along the elements. These time-varying fields radiate away from the antenna into space as a moving electromagnetic field wave. Conversely, during reception, the oscillating electric and magnetic fields of an incoming radio wave exert force on the electrons in the antenna elements, causing them to move back and forth, creating oscillating currents in the antenna.
Antennas may also contain reflective or directive elements or surfaces not connected to the transmitter or receiver, such as parasitic elements, parabolic reflectors or horns, which serve to direct the radio waves into a beam or other desired radiation pattern. Antennas can be designed to transmit or receive radio waves in all directions equally (omnidirectional antennas), or transmit them in a beam in a particular direction, and receive from that one direction only (directional or high gain antennas).
The first antennas were built in 1888 by German physicist Heinrich Hertz in his pioneering experiments to prove the existence of electromagnetic waves predicted by the theory of James Clerk Maxwell. Hertz placed dipole antennas at the focal point of parabolic reflectors for both transmitting and receiving. He published his work in Annalen der Physik und Chemie (vol. 36, 1889).
Contents |
Terminology
The words antenna (plural: antennas[1]) and aerial are used interchangeably; but usually a rigid metallic structure is termed an antenna and a wire format is called an aerial. In the United Kingdom and other British English speaking areas the term aerial is more common, even for rigid types. The noun aerial is occasionally written with a diaeresis mark—aërial—in recognition of the original spelling of the adjective aërial from which the noun is derived.
The origin of the word antenna relative to wireless apparatus is attributed to Italian radio pioneer Guglielmo Marconi. In 1895, while testing early radio apparatus in the Swiss Alps at Salvan, Switzerland in the Mont Blanc region, Marconi experimented with long wire 'aerials'. He used a 2.5 meter vertical pole, with a wire attached to the top running down to the transmitter, as a radiating and receiving aerial element. In Italian a tent pole is known as l'antenna centrale, and the pole with the wire was simply called l'antenna. Until then wireless radiating transmitting and receiving elements were known simply as aerials or terminals. Because of his prominence, Marconi's use of the word antenna (Italian for pole) spread among wireless researchers, and later to the general public.[2]
In common usage, the word antenna may refer broadly to an entire assembly including support structure, enclosure (if any), etc. in addition to the actual functional components. Especially at microwave frequencies, a receiving antenna may include not only the actual electrical antenna but an integrated preamplifier and/or mixer.
Overview
Antennas are required by any radio receiver or transmitter to couple its electrical connection to the electromagnetic field. Radio waves are electromagnetic waves which carry signals through the air (or through space) at the speed of light with almost no transmission loss. Radio transmitters and receivers are used to convey signals (information) in systems including broadcast (audio) radio, television, mobile telephones, wi-fi (WLAN) data networks, trunk lines and point-to-point communications links (telephone, data networks), satellite links, many remote controlled devices such as garage door openers, and wireless remote sensors, among many others. Radio waves are also used directly for measurements in technologies including RADAR, GPS, and radio astronomy. In each and every case, the transmitters and receivers involved require antennas, although these are sometimes hidden (such as the antenna inside an AM radio or inside a laptop computer equipped with wi-fi).
According to their applications and technology available, antennas generally fall in one of two categories:
- Omnidirectional or only weakly directional antennas which receive or radiate more or less in all directions. These are employed when the relative position of the other station is unknown or arbitrary. They are also used at lower frequencies where a directional antenna would be too large, or simply to cut costs in applications where a directional antenna isn't required.
- Directional or beam antennas which are intended to preferentially radiate or receive in a particular direction or directional pattern.
In common usage "omnidirectional" usually refers to all horizontal directions, typically with reduced performance in the direction of the sky or the ground (a truly isotropic radiator is not even possible). A "directional" antenna usually is intended to maximize its coupling to the electromagnetic field in the direction of the other station, or sometimes to cover a particular sector such as a 120° horizontal fan pattern in the case of a panel antenna at a cell site.
One example of omnidirectional antennas is the very common vertical antenna or whip antenna consisting of a metal rod (often, but not always, a quarter of a wavelength long). A dipole antenna is similar but consists of two such conductors extending in opposite directions, with a total length that is often, but not always, a half of a wavelength long. Dipoles are typically oriented horizontally in which case they are weakly directional: signals are reasonably well radiated toward or received from all directions with the exception of the direction along the conductor itself; this region is called the antenna blind cone or null.
Both the vertical and dipole antennas are simple in construction and relatively inexpensive. The dipole antenna, which is the basis for most antenna designs, is a balanced component, with equal but opposite voltages and currents applied at its two terminals through a balanced transmission line (or to a coaxial transmission line through a so-called balun). The vertical antenna, on the other hand, is a monopole antenna. It is typically connected to the inner conductor of a coaxial transmission line (or a matching network); the shield of the transmission line is connected to ground. In this way, the ground (or any large conductive surface) plays the role of the second conductor of a dipole, thereby forming a complete circuit.[3] Since monopole antennas rely on a conductive ground, a so-called grounding structure may be employed to provide a better ground contact to the earth or which itself acts as a ground plane to perform that function regardless of (or in absence of) an actual contact with the earth.
Antennas fancier than the dipole or vertical designs are usually intended to increase the directivity and consequently the gain of the antenna. This can be accomplished in many different ways leading to a plethora of antenna designs. The vast majority of designs are fed with a balanced line (unlike a monopole antenna) and are based on the dipole antenna with additional components (or elements) which increase its directionality.
For instance, a phased array consists of two or more simple antennas which are connected together through an electrical network. This often involves a number of parallel dipole antennas with a certain spacing. Depending on the relative phase introduced by the network, the same combination of dipole antennas can operate as a "broadside array" (directional normal to a line connecting the elements) or as an "end-fire array" (directional along the line connecting the elements). Antenna arrays may employ any basic (omnidirectional or weakly directional) antenna type, such as dipole, loop or slot antennas. These elements are often identical.
However a log-periodic dipole array consists of a number of dipole elements of different lengths in order to obtain a somewhat directional antenna having an extremely wide bandwidth: these are frequently used for television reception in fringe areas. The dipole antennas composing it are all considered "active elements" since they are all electrically connected together (and to the transmission line). On the other hand, a superficially similar dipole array, the Yagi-Uda Antenna (or simply "Yagi"), has only one dipole element with an electrical connection; the other so-called parasitic elements interact with the electromagnetic field in order to realize a fairly directional antenna but one which is limited to a rather narrow bandwidth. The Yagi antenna has similar looking parasitic dipole elements but which act differently due to their somewhat different lengths. There may be a number of so-called "directors" in front of the active element in the direction of propagation, and usually a single (but possibly more) "reflector" on the opposite side of the active element.
Greater directionality can be obtained using beam-forming techniques such as a parabolic reflector or a horn. Since the size of a directional antenna depends on it being large compared to the wavelength, very directional antennas of this sort are mainly feasible at UHF and microwave frequencies. On the other hand, at low frequencies (such as AM broadcast) where a practical antenna must be much smaller than a wavelength, significant directionality isn't even possible. A vertical antenna or loop antenna small compared to the wavelength is typically used, with the main design challenge being that of impedance matching. With a vertical antenna a loading coil at the base of the antenna may be employed to cancel the reactive component of impedance; small loop antennas are tuned with parallel capacitors for this purpose.
An antenna lead-in is the transmission line (or feed line) which connects the antenna to a transmitter or receiver. The antenna feed may refer to all components connecting the antenna to the transmitter or receiver, such as an impedance matching network in addition to the transmission line. In a so-called aperture antenna, such as a horn or parabolic dish, the "feed" may also refer to a basic antenna inside the entire system (normally at the focus of the parabolic dish or at the throat of a horn) which could be considered the one active element in that antenna system. A microwave antenna may also be fed directly from a waveguide in lieu of a (conductive) transmission line.
An antenna counterpoise or ground plane is a structure of conductive material which improves or substitutes for the ground. It may be connected to or insulated from the natural ground. In a monopole antenna, this aids in the function of the natural ground, particularly where variations (or limitations) of the characteristics of the natural ground interfere with its proper function. Such a structure is normally connected to the return connection of an unbalanced transmission line such as the shield of a coaxial cable.
An electromagnetic wave refractor in some aperture antennas is a component which due to its shape and position functions to selectively delay or advance portions of the electromagnetic wavefront passing through it. The refractor alters the spatial characteristics of the wave on one side relative to the other side. It can, for instance, bring the wave to a focus or alter the wave front in other ways, generally in order to maximize the directivity of the antenna system. This is the radio equivalent of an optical lens.
An antenna coupling network is a passive network (generally a combination of inductive and capacitive circuit elements) used for impedance matching in between the antenna and the transmitter or receiver. This may be used to improve the standing wave ratio in order to minimize losses in the transmission line (especially at higher frequencies and/or over longer distances) and to present the transmitter or receiver with a standard resistive impedance (such as 75 ohms) that it expects to see for optimum operation.
Reciprocity
It is a fundamental property of antennas that the electrical characteristics of an antenna described in the next section, such as gain, radiation pattern, impedance, bandwidth, resonant frequency and polarization, are the same whether the antenna is transmitting or receiving. For example, the "receiving pattern" (sensitivity as a function of direction) of an antenna when used for reception is identical to the radiation pattern of the antenna when it is driven and functions as a radiator. This is a consequence of the reciprocity theorem of electromagnetics. Therefore in discussions of antenna properties no distinction is usually made between receiving and transmitting terminology, and the antenna can be viewed as either transmitting or receiving, whichever is more convenient.
A necessary condition for the aforementioned reciprocity property is that the materials in the antenna and transmission medium are linear and reciprocal. Reciprocal (or bilateral) means that the material has the same response to an electric current or magnetic field in one direction, as it has to the field or current in the opposite direction. Most materials used in antennas meet these conditions, but some microwave antennas use high-tech components such as isolators and circulators, made of nonreciprocal materials such as ferrite or garnet. These can be used to give the antenna a different behavior on receiving than it has on transmitting, which can be useful in applications like radar.
Parameters
Antennas are characterized by a number of performance measures which a user would be concerned with in selecting or designing an antenna for a particular application. Chief among these relate to the directional characteristics (as depicted in the antenna's radiation pattern) and the resulting gain. Even in omnidirectional (or weakly directional) antennas, the gain can often be increased by concentrating more of its power in the horizontal directions, sacrificing power radiated toward the sky and ground. The antenna's power gain (or simply "gain") also takes into account the antenna's efficiency, and is often the primary figure of merit.
Resonant antennas are expected to be used around a particular resonant frequency; an antenna must therefore be built or ordered to match the frequency range of the intended application. A particular antenna design will present a particular feedpoint impedance. While this may affect the choice of an antenna, an antenna's impedance can also be adapted to the desired impedance level of a system using an matching network while maintaining the other characteristics (except for a possible loss of efficiency).
Although these parameters can be measured in principle, such measurements are difficult and require very specialized equipment. Beyond tuning a transmitting antenna using an SWR meter, the typical user will depend on theoretical predictions based on the antenna design and/or on claims of a vendor.
An antenna transmits and receives radio waves with a particular polarization which can be reoriented by tilting the axis of the antenna in many (but not all) cases. The physical size of an antenna is often a practical issue, particularly at lower frequencies (longer wavelengths). Highly directional antennas need to be significantly larger than the wavelength. Resonant antennas use a conductor, or a pair of conductors, each of which is about one quarter of the wavelength in length. Antennas that are required to be very small compared to the wavelength sacrifice efficiency and cannot be very directional. Fortunately at higher frequencies (UHF, microwaves) trading off performance to obtain a smaller physical size is usually not required.
Resonant antennas
While there are broadband designs for antennas, the vast majority of antennas are based on the half-wave dipole which has a particular resonant frequency. At its resonant frequency, the wavelength (figured by dividing the speed of light by the resonant frequency) is slightly over twice the length of the half-wave dipole (thus the name). The quarter-wave vertical antenna consists of one arm of a half-wave dipole, with the other arm replaced by a connection to ground or an equivalent ground plane (or counterpoise). A Yagi-Uda array consists of a number of resonant dipole elements, only one of which is directly connected to the transmission line. The quarter-wave elements of a dipole or vertical antenna imitate a series-resonant electrical element, since if they are driven at the resonant frequency a standing wave is created with the peak current at the feed-point and the peak voltage at the far end.
A common misconception is that the ability of a resonant antenna to transmit (or receive) fails at frequencies far from the resonant frequency. The reason a dipole antenna needs to be used at the resonant frequency has to do with the impedance match between the antenna and the transmitter or receiver (and its transmission line). For instance, a dipole using a fairly thin conductor[4] will have a purely resistive feedpoint impedance of about 63 ohms at its design frequency. Feeding that antenna with a current of 1 ampere will require 63 volts of RF, and the antenna will radiate 63 watts (ignoring losses) of radio frequency power. If that antenna is driven with 1 ampere at a frequency 20% higher, it will still radiate as efficiently but in order to do that about 200 volts would be required due to the change in the antenna's impedance which is now largely reactive (voltage out of phase with the current). A typical transmitter would not find that impedance acceptable and would deliver much less than 63 watts to it; the transmission line would be operating at a high (poor) standing wave ratio. But using an appropriate matching network, that large reactive impedance could be converted to a resistive impedance satisfying the transmitter and accepting the available power of the transmitter.
This principle is used to construct vertical antennas substantially shorter than the 1/4 wavelength at which the antenna is resonant. By adding an inductance in series with the vertical antenna (a so-called loading coil) the capacitative reactance of this antenna can be cancelled leaving a pure resistance which can then be matched to the transmission line. Sometimes the resulting resonant frequency of such a system (antenna plus matching network) is described using the construct of "electrical length" and the use of a shorter antenna at a lower frequency than its resonant frequency is termed "electrical lengthening". For example, at 30 MHz (wavelength = 10 meters) a true resonant monopole would be almost 2.5 meters (1/4 wavelength) long, and using an antenna only 1.5 meters tall would require the addition of a loading coil. Then it may be said that the coil has "lengthened" the antenna to achieve an "electrical length" of 2.5 meters, that is, 1/4 wavelength at 30 MHz where the combined system now resonates. However, the resulting resistive impedance achieved will be quite a bit lower than the impedance of a resonant monopole, likely requiring further impedance matching.
Current and voltage distribution
The antenna conductors have the lowest feed-point impedance at the resonant frequency where they are just under 1/4 wavelength long; two such conductors in line fed differentially thus realizes the familiar "half-wave dipole". When fed with an RF current at the resonant frequency, the quarter wave element contains a standing wave with the voltage and current largely (but not exactly) in phase quadrature, as would be obtained using a quarter wave stub of transmission line. The current reaches a minimum at the end of the element (where it has nowhere to go!) and is maximum at the feed-point. The voltage, on the other hand, is the greatest at the end of the conductor and reaches a minimum (but not zero) at the feedpoint. Making the conductor shorter or longer than 1/4 wavelength means that the voltage pattern reaches its minimum somewhere beyond the feed-point, so that the feed-point has a higher voltage and thus sees a higher impedance, as we have noted. Since that voltage pattern is almost in phase quadrature with the current, the impedance seen at the feed-point is not only much higher but mainly reactive.
It can be seen that if such an element is resonant at f0 to produce such a standing wave pattern, then feeding that element with 3f0 (whose wavelength is 1/3 that of f0) will lead to a standing wave pattern in which the voltage is likewise a minimum at the feed-point (and the current at a maximum there). Thus, an antenna element is also resonant when its length is 3/4 of a wavelength (3/2 wavelength for a complete dipole). This is true for all odd multiples of 1/4 wavelength, where the feed-point impedance is purely resistive, though larger than the resistive impedance of the 1/4 wave element. Although such an antenna is resonant and works perfectly well at the higher frequency, the antenna radiation pattern is also altered compared to the half-wave dipole.
The use of a monopole or dipole at odd multiples of the fundamental resonant frequency, however, does not extend to even multiples (thus a 1/2 wavelength monopole or 1 wavelength dipole). Now the voltage standing wave is at its peak at the feed-point, while that of the current (which must be zero at the end of the conductor) is at a minimum (but not exactly zero). The antenna is anti-resonant at this frequency. Although the reactance at the feedpoint can be cancelled using such an element length, the feed-point impedance is very high, and is highly dependent on the diameter of the conductor (which makes only a small difference at the actual resonant frequency). Such an antenna does not match the much lower characteristic impedance of available transmission lines, and is generally not used. However some equipment where transmission lines are not involved which desire a high driving point impedance may take advantage of this anti-resonance.
Bandwidth
Although a resonant antenna has a purely resistive feed-point impedance at a particular frequency, many (if not most) applications require using an antenna over a range of frequencies. An antenna's bandwidth specifies the range of frequencies over which its performance does not suffer due a poor impedance match. Also in the case of a Yagi-Uda array, the use of the antenna very far away from its design frequency reduces the antenna's directivity, thus reducing the usable bandwidth regardless of impedance matching.
Except for the latter concern, the resonant frequency of a resonant antenna can always be altered by adjusting a suitable matching network. To do this efficiently one would require remotely adjusting a matching network at the site of the antenna, since simply adjusting a matching network at the transmitter (or receiver) would leave the transmission line with a poor standing wave ratio.
Instead, it is often desired to have an antenna whose impedance does not vary so greatly over a certain bandwidth. It turns out that the amount of reactance seen at the terminals of a resonant antenna when the frequency is shifted, say, by 5%, depends very much on the diameter of the conductor used. A long thin wire used as a half-wave dipole (or quarter wave monopole) will have a reactance significantly greater than the resistive impedance it has at resonance, leading to a poor match and generally unacceptable performance. Making the element using a tube of a diameter perhaps 1/50 of its length, however, results in a reactance at this altered frequency which is not so great, and a much less serious mismatch which will only modestly damage the antenna's net performance. Thus rather thick tubes are typically used for the solid elements of such antennas, including Yagi-Uda arrays.
Rather than just using a thick tube, there are similar techniques used to the same effect such as replacing thin wire elements with cages to simulate a thicker element. This widens the bandwidth of the resonance. On the other hand, amateur radio antennas need to operate over several bands which are widely separated from each other. This can often be accomplished simply by connecting resonant elements for the different bands in parallel. Most of the transmitter's power will flow into the resonant element while the others present a high (reactive) impedance and draw little current from the same voltage. A popular solution uses so-called traps consisting of parallel resonant circuits which are strategically placed in breaks along each antenna element. When used at one particular frequency band the trap presents a very high impedance (parallel resonance) effectively truncating the element at that length, making it a proper resonant antenna. At a lower frequency the trap allows the full length of the element to be employed, albeit with a shifted resonant frequency due to the inclusion of the trap's net reactance at that lower frequency.
The bandwidth characteristics of a resonant antenna element can be characterized according to its Q, just as one uses to characterize the sharpness of an L-C resonant circuit. However it is often assumed that there is an advantage in an antenna having a high Q. After all, Q is short for "quality factor" and a low Q typically signifies excessive loss (due to unwanted resistance) in a resonant L-C circuit. However this understanding does not apply to resonant antennas where the resistance involved is the radiation resistance, a desired quantity which removes energy from the resonant element in order to radiate it (the purpose of an antenna, after all!). The Q is a measure of the ratio of reactance to resistance, so with a fixed radiation resistance (an element's radiation resistance is almost independent of its diameter) a greater reactance off-resonance corresponds to the poorer bandwidth of a very thin conductor. The Q of such a narrowband antenna can be as high as 15. On the other hand a thick element presents less reactance at an off-resonant frequency, and consequently a Q as low as 5. These two antennas will perform equivalently at the resonant frequency, but the second antenna will perform over a bandwidth 3 times as wide as the "hi-Q" antenna consisting of a thin conductor.
Gain
Gain is a parameter which measures the degree of directivity of the antenna's radiation pattern. A high-gain antenna will preferentially radiate in a particular direction. Specifically, the antenna gain, or power gain of an antenna is defined as the ratio of the intensity (power per unit surface) radiated by the antenna in the direction of its maximum output, at an arbitrary distance, divided by the intensity radiated at the same distance by a hypothetical isotropic antenna.
The gain of an antenna is a passive phenomenon - power is not added by the antenna, but simply redistributed to provide more radiated power in a certain direction than would be transmitted by an isotropic antenna. An antenna designer must take into account the application for the antenna when determining the gain. High-gain antennas have the advantage of longer range and better signal quality, but must be aimed carefully in a particular direction. Low-gain antennas have shorter range, but the orientation of the antenna is relatively inconsequential. For example, a dish antenna on a spacecraft is a high-gain device that must be pointed at the planet to be effective, whereas a typical Wi-Fi antenna in a laptop computer is low-gain, and as long as the base station is within range, the antenna can be in any orientation in space. It makes sense to improve horizontal range at the expense of reception above or below the antenna. Thus most antennas labelled "omnidirectional" really have some gain.[5]
In practice, the half-wave dipole is taken as a reference instead of the isotropic radiator. The gain is then given in dBd (decibels over dipole):
-
- NOTE: 0 dBd = 2.15 dBi. It is vital in expressing gain values that the reference point be included. Failure to do so can lead to confusion and error.
Effective area or aperture
The effective area or effective aperture of a receiving antenna expresses the portion of the power of a passing electromagnetic wave which it delivers to its terminals, expressed in terms of an equivalent area. For instance, if a radio wave passing a given location has a flux of 1 pW / m2 (10−12 watts per square meter) and an antenna has an effective area of 12 m2, then the antenna would deliver 12 pW of RF power to the receiver (30 microvolts rms at 75 ohms). Since the receiving antenna is not equally sensitive to signals received from all directions, the effective area is a function of the direction to the source.
Due to reciprocity (discussed above) the gain of an antenna used for transmitting must be proportional to its effective area when used for receiving. Consider an antenna with no loss, that is, one whose electrical efficiency is 100%. It can be shown that its effective area averaged over all directions must be equal to λ2/4π, the wavelength squared divided by 4π. Gain is defined such that the average gain over all directions for an antenna with 100% electrical efficiency is equal to 1. Therefore the effective area Aeff in terms of the gain G in a given direction is given by:
For an antenna with an efficiency of less than 100%, both the effective area and gain are reduced by that same amount. Therefore the above relationship between gain and effective area still holds. These are thus two different ways of expressing the same quantity. Aeff is especially convenient when computing the power that would be received by an antenna of a specified gain, as illustrated by the above example.
Radiation pattern
The radiation pattern of an antenna is a plot of the relative field strength of the radio waves emitted by the antenna at different angles. It is typically represented by a three dimensional graph, or polar plots of the horizontal and vertical cross sections. The pattern of an ideal isotropic antenna, which radiates equally in all directions, would look like a sphere. Many nondirectional antennas, such as monopoles and dipoles, emit equal power in all horizontal directions, with the power dropping off at higher and lower angles; this is called an omnidirectional pattern and when plotted looks like a torus or donut.
The radiation of many antennas shows a pattern of maxima or "lobes" at various angles, separated by "nulls", angles where the radiation falls to zero. This is because the radio waves emitted by different parts of the antenna typically interfere, causing maxima at angles where the radio waves arrive at distant points in phase, and zero radiation at other angles where the radio waves arrive out of phase. In a directional antenna designed to project radio waves in a particular direction, the lobe in that direction is designed larger than the others and is called the "main lobe". The other lobes usually represent unwanted radiation and are called "sidelobes". The axis through the main lobe is called the "principle axis" or "boresight axis".
Impedance
As an electro-magnetic wave travels through the different parts of the antenna system (radio, feed line, antenna, free space) it may encounter differences in impedance (E/H, V/I, etc.). At each interface, depending on the impedance match, some fraction of the wave's energy will reflect back to the source,[6] forming a standing wave in the feed line. The ratio of maximum power to minimum power in the wave can be measured and is called the standing wave ratio (SWR). A SWR of 1:1 is ideal. A SWR of 1.5:1 is considered to be marginally acceptable in low power applications where power loss is more critical, although an SWR as high as 6:1 may still be usable with the right equipment. Minimizing impedance differences at each interface (impedance matching) will reduce SWR and maximize power transfer through each part of the antenna system.
Complex impedance of an antenna is related to the electrical length of the antenna at the wavelength in use. The impedance of an antenna can be matched to the feed line and radio by adjusting the impedance of the feed line, using the feed line as an impedance transformer. More commonly, the impedance is adjusted at the load (see below) with an antenna tuner, a balun, a matching transformer, matching networks composed of inductors and capacitors, or matching sections such as the gamma match.
Efficiency
Efficiency of a transmitting antenna is the ratio of power actually radiated (in all directions) to the power absorbed by the antenna terminals. The power supplied to the antenna terminals which is not radiated is converted into heat. This is usually through loss resistance in the antenna's conductors, but can also be due to dielectric or magnetic core losses in antennas (or antenna systems) using such components. Such loss effectively robs power from the transmitter, requiring a stronger transmitter in order to transmit a signal of a given strength.
For instance, if a transmitter delivers 100 W into an antenna having an efficiency of 80%, then the antenna will radiate 80 W as radio waves and produce 20 W of heat. In order to radiate 100 W of power, one would need to use a transmitter capable of supplying 125 W to the antenna. Note that antenna efficiency is a separate issue from impedance matching, which may also reduce the amount of power radiated using a given transmitter. If an SWR meter reads 150 W of incident power and 50 W of reflected power, that means that 100 W have actually been absorbed by the antenna (ignoring transmission line losses). How much of that power has actually been radiated cannot be directly determined through electrical measurements at (or before) the antenna terminals, but would require (for instance) careful measurement of field strength. Fortunately the loss resistance of antenna conductors such as aluminum rods can be calculated and the efficiency of an antenna using such materials predicted.
However loss resistance will generally affect the feedpoint impedance, adding to its resistive (real) component. That resistance will consist of the sum of the radiation resistance Rr and the loss resistance Rloss. If an rms current I is delivered to the terminals of an antenna, then a power of I2Rr will be radiated and a power of I2Rloss will be lost as heat. Therefore the efficiency of an antenna is equal to Rr / (Rr + Rloss). Of course only the total resistance Rr + Rloss can be directly measured.
According to reciprocity, the efficiency of an antenna, when used as a receiving antenna, is identical to the efficiency as defined above. The power that an antenna will deliver to a receiver (with a proper impedance match) is reduced by the same amount. However often in a receiving application, inefficiency of an antenna may be of lesser consequence or even of no consequence, notably at lower frequencies or when used to receive signals in "crowded" bands. That is true in cases where the received signal competes not against receiver noise, but against atmospheric noise or interference received by the antenna itself. The loss within the antenna will affect the intended signal and the noise/interference identically, leading to no reduction in signal to noise ratio (SNR). According to the graph shown illustrating the frequency dependence of atmospheric and man-made noise, one can see that using a receiving antenna with an efficiency of only 10% at frequencies below 10 MHz will still supply a signal to the receiver which includes noise well above the thermal limit. A decent RF amplifier in the receiver will not significantly add to this noise level or reduce the resulting SNR.
This is fortunate, since antennas at lower frequencies which are not rather large (a good fraction of a wavelength in size) are inevitably inefficient (due to the small radiation resistance Rr of small antennas). Most AM broadcast radios (except for car radios) take advantage of this principle by including a small loop antenna for reception which has an extremely poor efficiency. Using such an inefficient antenna at this low frequency (530–1650 kHz) thus has little effect on the receiver's net performance, but simply requires greater amplification by the receiver's electronics. Contrast this tiny component to the massive and very tall towers used at AM broadcast stations for transmitting at the very same frequency, where every percentage point of reduced antenna efficiency entails a substantial cost.
The definition of antenna gain or power gain already includes the effect of the antenna's efficiency. Therefore if one is trying to radiate a signal toward a receiver using a transmitter of a given power, one need only compare the gain of various antennas rather than considering the efficiency as well. This is likewise true for a receiving antenna at very high (especially microwave) frequencies, where the point is to receive a signal which is strong compared to the receiver's noise temperature. However in the case of a directional antenna used for receiving signals with the intention of rejecting interference from different directions, one is no longer concerned with the antenna efficiency, as discussed above. In this case, rather than quoting the antenna gain, one would be more concerned with the directive gain which does not include the effect of antenna (in)efficiency. The directive gain of an antenna can be computed from the published gain divided by the antenna's efficiency.
Polarization
The polarization of an antenna is the orientation of the electric field (E-plane) of the radio wave with respect to the Earth's surface and is determined by the physical structure of the antenna and by its orientation. It has nothing in common with antenna directionality terms: "horizontal", "vertical", and "circular". Thus, a simple straight wire antenna will have one polarization when mounted vertically, and a different polarization when mounted horizontally. "Electromagnetic wave polarization filters" are structures which can be employed to act directly on the electromagnetic wave to filter out wave energy of an undesired polarization and to pass wave energy of a desired polarization.
Reflections generally affect polarization. For radio waves the most important reflector is the ionosphere - signals which reflect from it will have their polarization changed unpredictably. For signals which are reflected by the ionosphere, polarization cannot be relied upon. For line-of-sight communications for which polarization can be relied upon, it can make a large difference in signal quality to have the transmitter and receiver using the same polarization; many tens of dB difference are commonly seen and this is more than enough to make the difference between reasonable communication and a broken link.
Polarization is largely predictable from antenna construction but, especially in directional antennas, the polarization of side lobes can be quite different from that of the main propagation lobe. For radio antennas, polarization corresponds to the orientation of the radiating element in an antenna. A vertical omnidirectional WiFi antenna will have vertical polarization (the most common type). An exception is a class of elongated waveguide antennas in which vertically placed antennas are horizontally polarized. Many commercial antennas are marked as to the polarization of their emitted signals.
Polarization is the sum of the E-plane orientations over time projected onto an imaginary plane perpendicular to the direction of motion of the radio wave. In the most general case, polarization is elliptical, meaning that the polarization of the radio waves varies over time. Two special cases are linear polarization (the ellipse collapses into a line) and circular polarization (in which the two axes of the ellipse are equal). In linear polarization the antenna compels the electric field of the emitted radio wave to a particular orientation. Depending on the orientation of the antenna mounting, the usual linear cases are horizontal and vertical polarization. In circular polarization, the antenna continuously varies the electric field of the radio wave through all possible values of its orientation with regard to the Earth's surface. Circular polarizations, like elliptical ones, are classified as right-hand polarized or left-hand polarized using a "thumb in the direction of the propagation" rule. Optical researchers use the same rule of thumb, but pointing it in the direction of the emitter, not in the direction of propagation, and so are opposite to radio engineers' use.
In practice, regardless of confusing terminology, it is important that linearly polarized antennas be matched, lest the received signal strength be greatly reduced. So horizontal should be used with horizontal and vertical with vertical. Intermediate matchings will lose some signal strength, but not as much as a complete mismatch. Transmitters mounted on vehicles with large motional freedom commonly use circularly polarized antennas so that there will never be a complete mismatch with signals from other sources.
Impedance matching
Maximum power transfer requires matching the impedance of an antenna system (as seen looking into the transmission line) to the complex conjugate of the impedance of the receiver or transmitter. In the case of a transmitter, however, the desired matching impedance might not correspond to the dynamic output impedance of the transmitter as analyzed as a source impedance but rather the design value (typically 50 ohms) required for efficient and safe operation of the transmitting circuitry. The intended impedance is normally resistive but a transmitter (and some receivers) may have additional adjustments to cancel a certain amount of reactance in order to "tweak" the match. When a transmission line is used in between the antenna and the transmitter (or receiver) one generally would like an antenna system whose impedance is resistive and near the characteristic impedance of that transmission line in order to minimize the standing wave ratio (SWR) and the increase in transmission line losses it entails, in addition to supplying a good match at the transmitter or receiver itself.
Antenna tuning generally refers to cancellation of any reactance seen at the antenna terminals, leaving only a resistive impedance which might or might not be exactly the desired impedance (that of the transmission line). Although an antenna may be designed to have a purely resistive feedpoint impedance (such as a dipole 97% of a half wavelength long) this might not be exactly true at the frequency that it is eventually used at. In some cases the physical length of the antenna can be "trimmed" to obtain a pure resistance. On the other hand, the addition of a series inductance or parallel capacitance can be used to cancel a residual capacitative or inductive reactance, respectively.
In some cases this is done in a more extreme manner, not simply to cancel a small amount of residual reactance, but to resonate an antenna whose resonance frequency is quite different than the intended frequency of operation. For instance, a "whip antenna" can be made significantly shorter than 1/4 wavelength long, for practical reasons, and then resonated using a so-called loading coil. This physically large inductor at the base of the antenna has an inductive reactance which is the opposite of the capacitative reactance that such a vertical antenna has at the desired operating frequency. The result is a pure resistance seen at feedpoint of the loading coil; unfortunately that resistance is somewhat lower than would be desired to match commercial coax.
So an additional problem beyond canceling the unwanted reactance is of matching the remaining resistive impedance to the characteristic impedance of the transmission line. In principle this can always be done with a transformer, however the turns ratio of a transformer is not adjustable. A general matching network with at least two adjustments can be made to correct both components of impedance. Matching networks using discrete inductors and capacitors will have losses associated with those components, and will have power restrictions when used for transmitting. Avoiding these difficulties, commercial antennas are generally designed with fixed matching elements and/or feeding strategies to get an approximate match to standard coax, such as 50 or 75 Ohms. Antennas based on the dipole (rather than vertical antennas) should include a balun in between the transmission line and antenna element, which may be integrated into any such matching network.
Another extreme case of impedance matching occurs when using a small loop antenna (usually, but not always, for receiving) at a relatively low frequency where it appears almost as a pure inductor. Resonating such an inductor with a capacitor at the frequency of operation not only cancels the reactance but greatly magnifies the very small radiation resistance of such a loop. This is implemented in most AM broadcast receivers, with a small ferrite loop antenna resonated by a capacitor which is varied along with the receiver tuning in order to maintain resonance over the AM broadcast band
Basic antenna models
There are many variations of antennas. Below are a few basic models. More can be found in Category:Radio frequency antenna types.
- The isotropic radiator is a purely theoretical antenna that radiates equally in all directions. It is considered to be a point in space with no dimensions and no mass. This antenna cannot physically exist, but is useful as a theoretical model for comparison with all other antennas. Most antennas' gains are measured with reference to an isotropic radiator, and are rated in dBi (decibels with respect to an isotropic radiator).
- The dipole antenna is simply two wires pointed in opposite directions arranged either horizontally or vertically, with one end of each wire connected to the radio and the other end hanging free in space. Since this is the simplest practical antenna, it is also used as a reference model for other antennas; gain with respect to a dipole is labeled as dBd. Generally, the dipole is considered to be omnidirectional in the plane perpendicular to the axis of the antenna, but it has deep nulls in the directions of the axis. Variations of the dipole include the folded dipole, the half wave antenna, the ground plane antenna, the whip, and the J-pole.
- The Yagi-Uda antenna is a directional variation of the dipole with parasitic elements added which are functionality similar to adding a reflector and lenses (directors) to focus a filament light bulb.
- The random wire antenna is simply a very long (at least one quarter wavelength) wire with one end connected to the radio and the other in free space, arranged in any way most convenient for the space available. Folding will reduce effectiveness and make theoretical analysis extremely difficult. (The added length helps more than the folding typically hurts.) Typically, a random wire antenna will also require an antenna tuner, as it might have a random impedance that varies non-linearly with frequency.
- The horn antenna is used where high gain is needed, the wavelength is short (microwave) and space is not an issue. Horns can be narrow band or wide band, depending on their shape. A horn can be built for any frequency, but horns for lower frequencies are typically impractical. Horns are also frequently used as reference antennas.
- The parabolic antenna consists of an active element at the focus of a parabolic reflector to reflect the waves into a plane wave. Like the horn it is used for high gain, microwave applications, such as satellite dishes.
- The patch antenna consists mainly of a square conductor mounted over a groundplane. Another example of a planar antenna is the tapered slot antenna (TSA), as the Vivaldi-antenna.
Practical antennas
Although any circuit can radiate if driven with a signal of high enough frequency, most practical antennas are specially designed to radiate efficiently at a particular frequency. An example of an inefficient antenna is the simple Hertzian dipole antenna, which radiates over wide range of frequencies and is useful for its small size. A more efficient variation of this is the half-wave dipole, which radiates with high efficiency when the signal wavelength is twice the electrical length of the antenna.
One of the goals of antenna design is to minimize the reactance of the device so that it appears as a resistive load. An "antenna inherent reactance" includes not only the distributed reactance of the active antenna but also the natural reactance due to its location and surroundings (as for example, the capacity relation inherent in the position of the active antenna relative to ground). Reactance can be eliminated by operating the antenna at its resonant frequency, when its capacitive and inductive reactances are equal and opposite, resulting in a net zero reactive current. If this is not possible, compensating inductors or capacitors can instead be added to the antenna to cancel its reactance as far as the source is concerned.
Once the reactance has been eliminated, what remains is a pure resistance, which is the sum of two parts: the ohmic resistance of the conductors, and the radiation resistance. Power absorbed by the ohmic resistance becomes waste heat, and that absorbed by the radiation resistance becomes radiated electromagnetic energy. The greater the ratio of radiation resistance to ohmic resistance, the more efficient the antenna.
Effect of ground
Antennas are typically used in an environment where other objects are present that may have an effect on their performance. Height above ground has a very significant effect on the radiation pattern of some antenna types.
At frequencies used in antennas, the ground behaves mainly as a dielectric. The conductivity of ground at these frequencies is negligible. When an electromagnetic wave arrives at the surface of an object, two waves are created: one enters the dielectric and the other is reflected. If the object is a conductor, the transmitted wave is negligible and the reflected wave has almost the same amplitude as the incident one. When the object is a dielectric, the fraction reflected depends (among other things) on the angle of incidence. When the angle of incidence is small (that is, the wave arrives almost perpendicularly) most of the energy traverses the surface and very little is reflected. When the angle of incidence is near 90° (grazing incidence) almost all the wave is reflected.
Most of the electromagnetic waves emitted by an antenna to the ground below the antenna at moderate (say < 60°) angles of incidence enter the earth and are absorbed (lost). But waves emitted to the ground at grazing angles, far from the antenna, are almost totally reflected. At grazing angles, the ground behaves as a mirror. Quality of reflection depends on the nature of the surface. When the irregularities of the surface are smaller than the wavelength, reflection is good.
This means that the receptor "sees" the real antenna and, under the ground, the image of the antenna reflected by the ground. If the ground has irregularities, the image will appear fuzzy.
If the receiver is placed at some height above the ground, waves reflected by ground will travel a little longer distance to arrive to the receiver than direct waves. The distance will be the same only if the receiver is close to ground.
In the drawing at right, the angle has been drawn 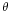 far bigger than in reality. The distance between the antenna and its image is
far bigger than in reality. The distance between the antenna and its image is 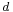 .
.
The situation is a bit more complex because the reflection of electromagnetic waves depends on the polarization of the incident wave. As the refractive index of the ground (average value 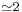 ) is bigger than the refractive index of the air (
) is bigger than the refractive index of the air (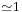 ), the direction of the component of the electric field parallel to the ground inverses at the reflection. This is equivalent to a phase shift of
), the direction of the component of the electric field parallel to the ground inverses at the reflection. This is equivalent to a phase shift of 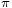 radians or 180°. The vertical component of the electric field reflects without changing direction. This sign inversion of the parallel component and the non-inversion of the perpendicular component would also happen if the ground were a good electrical conductor.
radians or 180°. The vertical component of the electric field reflects without changing direction. This sign inversion of the parallel component and the non-inversion of the perpendicular component would also happen if the ground were a good electrical conductor.
This means that a receiving antenna "sees" the image antenna with the current in the same direction if the antenna is vertical or with the current inverted if the antenna is horizontal.
For a vertical polarized emission antenna the far electric field of the electromagnetic wave produced by the direct ray plus the reflected ray is:
The sign inversion for the parallel field case just changes a cosine to a sine:
In these two equations:
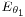 is the electrical field radiated by the antenna if there were no ground.
is the electrical field radiated by the antenna if there were no ground.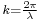 is the wave number.
is the wave number.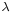 is the wave length.
is the wave length.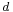 is the distance between antenna and its image (twice the height of the center of the antenna).
is the distance between antenna and its image (twice the height of the center of the antenna).
For emitting and receiving antennas situated near the ground (in a building or on a mast) far from each other, distances traveled by direct and reflected rays are nearly the same. There is no induced phase shift. If the emission is polarized vertically, the two fields (direct and reflected) add and there is maximum of received signal. If the emission is polarized horizontally, the two signals subtract and the received signal is minimum. This is depicted in the image at right. In the case of vertical polarization, there is always a maximum at earth level (left pattern). For horizontal polarization, there is always a minimum at earth level. Note that in these drawings the ground is considered as a perfect mirror, even for low angles of incidence. In these drawings, the distance between the antenna and its image is just a few wavelengths. For greater distances, the number of lobes increases.
Note that the situation is different—and more complex—if reflections in the ionosphere occur. This happens over very long distances (thousands of kilometers). There is not a direct ray but several reflected rays that add with different phase shifts.
This is the reason why almost all public address radio emissions have vertical polarization. As public users are near ground, horizontal polarized emissions would be poorly received. Observe household and automobile radio receivers. They all have vertical antennas or horizontal ferrite antennas for vertical polarized emissions. In cases where the receiving antenna must work in any position, as in mobile phones, the emitter and receivers in base stations use circular polarized electromagnetic waves.
Classical (analog) television emissions are an exception. They are almost always horizontally polarized, because the presence of buildings makes it unlikely that a good emitter antenna image will appear. However, these same buildings reflect the electromagnetic waves and can create ghost images. Using horizontal polarization, reflections are attenuated because of the low reflection of electromagnetic waves whose magnetic field is parallel to the dielectric surface near the Brewster's angle. Vertically polarized analog television has been used in some rural areas. In digital terrestrial television reflections are less obtrusive, due to the inherent robustness of digital signalling and built-in error correction.
Mutual impedance and interaction between antennas
Current circulating in any antenna induces currents in all others. One can postulate a mutual impedance 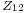 between two antennas that has the same significance as the
between two antennas that has the same significance as the 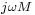 in ordinary coupled inductors. The mutual impedance
in ordinary coupled inductors. The mutual impedance 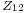 between two antennas is defined as:
between two antennas is defined as:
where 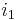 is the current flowing in antenna 1 and
is the current flowing in antenna 1 and 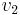 is the voltage that would have to be applied to antenna 2–with antenna 1 removed–to produce the current in the antenna 2 that was produced by antenna 1.
is the voltage that would have to be applied to antenna 2–with antenna 1 removed–to produce the current in the antenna 2 that was produced by antenna 1.
From this definition, the currents and voltages applied in a set of coupled antennas are:
where:
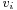 is the voltage applied to the antenna
is the voltage applied to the antenna 
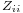 is the impedance of antenna
is the impedance of antenna 
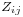 is the mutual impedance between antennas
is the mutual impedance between antennas  and
and 
Note that, as is the case for mutual inductances,
This is a consequence of Lorentz reciprocity. If some of the elements are not fed (there is a short circuit instead a feeder cable), as is the case in television antennas (Yagi-Uda antennas), the corresponding 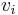 are zero. Those elements are called parasitic elements. Parasitic elements are unpowered elements that either reflect or absorb and reradiate RF energy.
are zero. Those elements are called parasitic elements. Parasitic elements are unpowered elements that either reflect or absorb and reradiate RF energy.
In some geometrical settings, the mutual impedance between antennas can be zero. This is the case for crossed dipoles used in circular polarization antennas.
Antenna gallery
Antennas and antenna arrays
Antennas and supporting structures
Diagrams as part of a system
See also
- Amateur radio
- Antenna measurement
- AWX antenna
- Category:Radio frequency antenna types
- Category:Radio frequency propagation
- Cellular repeater
- DXing
- Electromagnetism
- Mast radiator
- Mobile modem
- Numerical Electromagnetics Code
- Radio masts and towers
- Radio telescope
- RF connector
- Satellite television
- Smart antenna
- Television antenna
- TETRA
- Whip antenna
- Wi-Fi
Notes
- ^ In the context of engineering and physics, the plural of antenna is antennas, and it has been this way since about 1950 (or earlier), when a cornerstone textbook in this field, Antennas, was published by John D. Kraus of the Ohio State University. Besides the title, Dr. Kraus noted this in a footnote on the first page of his book. Insects may have "antennae", but this form is not used in the context of electronics.
- ^ "Salvan: Cradle of Wireless, How Marconi Conducted Early Wireless Experiments in the Swiss Alps", Fred Gardiol & Yves Fournier, Microwave Journal, February 2006, pp. 124-136.
- ^ Tesla said during the development of radio that "One of the terminals of the source would be connected to Earth [as a electric ground connection ...] the other to an insulated body of large surface. For more information, see "On Light and Other High Frequency Phenomena". Delivered before the Franklin Institute, Philadelphia, February 1893, and before the National Electric Light Association, St. Louis, Missouri, March 1893.
- ^ This example assumes a length to diameter ratio of 1000.
- ^ "Guide to Wi-Fi Wireless Network Antenna Selection.". NetworkBits.net. http://networkbits.net/wireless-printing/wireless-network-antenna-guide/. Retrieved April 8, 2008.
- ^ Impedance is caused by the same physics as refractive index in optics, although impedance effects are typically one dimensional, where effects of refractive index is three dimensional.
References
General references
- Antenna Theory (3rd edition), by C. Balanis, Wiley, 2005, ISBN 0-471-66782-X;
- Antenna Theory and Design (2nd edition), by W. Stutzman and G. Thiele, Wiley, 1997, ISBN 0-471-02590-9;
- Antennas (3rd edition), by J. Kraus and R. Marhefka, McGraw-Hill, 2001, ISBN 0-072-32103-2;
- Antennenbuch, by Karl Rothammel, publ. Franck'sche Verlagshandlung Stuttgart, 1991, ISBN 3-440-05853-0; other editions (in German)
- Antennas for portable Devices, Zhi Ning Chen (edited), John Wiley & Sons in March 2007
- Broadband Planar Antennas: Design and Applications, Zhi Ning Chen and M. Y. W. Chia, John Wiley & Sons in February 2006
- The ARRL Antenna Book (15th edition), ARRL, 1988, ISBN 0-87259-207-5
"Practical antenna" references
- Antenna Theory antenna-theory.com
- Patch Antenna: From Simulation to Realization EM Talk
- Why an Antenna Radiates at ARRL
- Why Antennas Radiate, Stuart G. Downs, WY6EE (PDF)
- Understanding electromagnetic fields and antenna radiation takes (almost) no math, Ron Schmitt, EDN Magazine, March 2 2000 (PDF)
- Tests of FM/VHF receiving antennas.
- http://www.tvantennasperth.com.au/Diyantennas.html :"Antenna Gain"
- Antennas: Generalities, Principle of operation, As electronic component, Hertz Marconi and Other types Antennas etc etc
Theory and simulations
- http://www.dipoleanimator.com
- EM Talk, "Microstrip Patch Antenna", (Theory and simulation of microstrip patch antenna)
- "Online Calculations and Conversions " Formulas for simulating and optimizing Antenna specs and placement
- "Microwave Antenna Design Calculator" Provides quick estimation of antenna size required for a given gain and frequency. 3 dB and 10 dB beamwidths are also derived; the calculator additionally gives the far-field range required for a given antenna.
- Sophocles J. Orfanidis, "Electromagnetic Waves and Antennas", Rutgers University (20 PDF Chaps. Basic theory, definitions and reference)
- Hans Lohninger, "Learning by Simulations: Physics: Coupled Radiators". vias.org, 2005. (ed. Interactive simulation of two coupled antennas)
- NEC Lab - NEC Lab is a tool that uses Numerical Electromagnetics Code and Artificial Intelligence to design and simulate antennas.
- Justin Smith "Aerials". A.T.V (Aerials and Television), 2009. (ed. Article on the (basic) theory and use of FM, DAB & TV aerials)
- Antennas Research Group, "Virtual (Reality) Antennas". Democritus University of Thrace, 2005.
- "Support > Knowledgebase > RF Basics > Antennas / Cables > dBi vs. dBd detail". MaxStream, Inc., 2005. (ed. How to measure antenna gain)
- Yagis and Log Periodics, Astrosurf article.
- Raines, J. K., "Virtual Outer Conductor for Linear Antennas," Microwave Journal, Vol. 52, No. 1, January, 2009, pp. 76–86
- Tests of FM/VHF receiving antennas.
- Effect of ground references
- Electronic Radio and Engineering. F.E. Terman. McGraw-Hill
- Lectures on physics. Feynman, Leighton and Sands. Addison-Wesley
- Classical Electricity and Magnetism. W. Panofsky and M. Phillips. Addison-Wesley
Patents and USPTO
- CLASS 343, Communication: Radio Wave Antenna
Further reading
- Antennas for Base Stations in Wireless Communications, edited by Zhi Ning Chen and Kwai-Man Luk, McGraw-Hill Companies, Inc, USA in May 2009
|
||||||||||||||
|
||||||||||||||||||||||||||||||||